5123. Град HOTPO

Последовательность града образуется следующим образом:

· Если n четно, то делим его на 2 и присваиваем n

· Если n нечетно, то умножим его на 3, прибавим 1 и присваиваем n

Утверждается, что для любого натурального числа n указанная последовательность всегда заканчивается циклом: 4, 2, 1, 4, 2, 1, ... Достаточно сказать, что при n = 1 последовательность заканчивается.

Напишите программу, которая определит наибольшее значение в последовательности для заданного числа n.

Вход. Первая строка содержит количество тестов t (1 ≤ t ≤ 100000). Каждый тест следует обработать независимо от других.

Каждый тест состоит из одной строки, содержащей два целых числа. Первое число указывает на номер теста. Вторым является число n (1 ≤ n ≤ 100000) – начальное число последовательности.

Выход. Для каждого теста выведите в отдельной строке его номер, пробел, и наибольшее число, встречающееся во всей последовательности начиная с n.

Пример входа	Пример выхода
4 1 1 2 3 3 9999 4 100000	1 1 2 16 3 101248 4 100000

РЕШЕНИЕ

рекурсия

Анализ алгоритма

В задаче достаточно промоделировать вычисление функции

f(n) = ,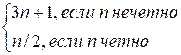

построив последовательность n, f(n), f(f(n)), …, 1. Остается найти максимальное значение в этой последовательности.

Реализация алгоритма

Реализуем функцию f(n).

int f(int n)

{

if (n % 2) return 3 * n + 1;

return n / 2;

}

Основная часть программы. Читаем входные данные.

scanf("%d",&tests);

while(tests--)

{

scanf("%d %d",&tn,&n);

mx = 1;

Генерируем последовательность n, f(n), f(f(n)), …, 1 и находим в ней наибольшее значение.

.

while(n > 1)

{

if (n > mx) mx = n;

n = f(n);

}

printf("%d %d\n",tn,mx);

}